Postulat I: o przyporządkowaniu operatorów wielkościom fizycznym.

Postulat I: o przyporządkowaniu operatorów wielkościom fizycznym. Operatory momentu pędu i energii.

„Każdej mierzalnej wielkości fizycznej przyporządkowany jest operator hermitowski.”

Operator hermitowski (sprzężony) – w algebrze liniowej i analizie funkcjonalnej rodzaj operatora odpowiadającego liniowemu i ciągłemu operatorowi przestrzeni Hilberta. Operator sprzężony hermitowsko względem operatora $A$ oznacza się przez $A^+$ i definiuje jako operator spełniający relację:

$\braket{ \psi | A^+ | \phi } = \braket{ \phi | A |\psi }^*$

co daje w rezultacie szczególną własność operatora hermitowskiego: $A^+ = A$

Przestrzeń Hilberta – rzeczywista lub zespolona wektorowa (w mechanice kwantowej zwykle zespolona) przestrzeń liniowa $H$ z określonym iloczynem skalarnym. Może mieć nieskończenie wiele wymiarów (termin ten nie ma nic wspólnego z fizycznym wymiarem układu).

Można wyróżnić trzy typy przyporządkowania w mechanice kwantowej:
● przyporządkowanie podstawowe
● przyporządkowanie wtórne
● przyporządkowanie nieklasyczne

Przyporządkowanie podstawowe:

Wielkości fizyczne	Reprezentacja klasyczna	Reprezentacja operatorowa
Położenie	$x \quad y \quad z$	$x \quad y \quad z$ operatory mnożenia przez liczbę
Pęd	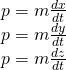$\\ p = m \frac{dx}{dt} \\ p = m \frac{dy}{dt} \\ p = m \frac{dz}{dt}$	$\\ p_x = -i\hbar \frac{\partial}{\partial x} \\ p_y = -i\hbar \frac{\partial}{\partial y} \\ p_z = -i\hbar \frac{\partial}{\partial z}$

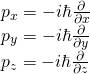
Przyporządkowanie wtórne:

Operator ten powstaje w wyniku działań matematycznych na podstawowych operatorach. Przykładem jest operator energii kinetycznej $T$ :
Kwadrat całkowitego pędu w fizyce klasycznej ma postać:

$\vec{p}^{\,2} = p_x^2 + p_y^2 + p_z^2$

W mechanice kwantowej ma postać:

$\vec{p}^{\,2} = - \hbar^2\nabla^2$

Energia kinetyczna w fizyce klasycznej wyraża się wzorem:

$T = \frac{p^2}{2m}$

Zatem postać operatora energii kinetycznej w mechanice kwantowej będzie wyglądać:

$T = -\frac{\hbar^2}{2m}\nabla^2$

Energia potencjalna zachowuje swoją klasyczną postać w mechanice kwantowej.

Przyporządkowanie nieklasyczne:

Przyporządkowanie te, odnosi się do tych wielkości fizycznych, które nie mają swojego klasycznego odpowiednika. Np. wewnętrzny moment pędu elektronu (spin) mierzony doświadczalnie wynosi $\frac{1}{2}\hbar$ . Jeżeli potraktować klasycznie elektron jako wirującą wokół osi kulkę to wynik wyjdzie bezsensowny (prędkość obrotowa elektronu byłaby o wiele większa od prędkości światła), dlatego operator spinu ma sens tylko w mechanice kwantowej.

Przyporządkowanie podstawowe:

Przyporządkowanie wtórne:

Przyporządkowanie nieklasyczne:

Related Articles

Popular Posts